Quantization of Damped Mechanical Systems Based on the Doubling of Degrees of Freedom

Received 18 Mar, 2025

Accepted 18 May, 2025

Published 19 May, 2025

Quantizing dissipative systems like damped harmonic oscillators remains an ongoing challenge in theoretical physics due to their non-conservative nature. This study addresses this issue by employing the method of doubling the degrees of freedom, transforming an open, dissipative system into a closed, conservative one through the introduction of a time-reversed mirror system. The aim is to derive a quantum model consistent with classical mechanics using the Hamilton-Jacobi formalism and to formulate an equivalent Schrödinger equation. Through canonical transformations and analytical solutions, we demonstrate that damping effectively vanishes in the quantum model. These results offer new insights into the quantization of non-conservative systems and contribute to the advancement of quantum open-system theory.

INTRODUCTION

Damped mechanical systems are essential in both classical and quantum physics, especially in the context of open quantum systems, yet they are notoriously difficult to quantize due to energy dissipation. Traditional quantization frameworks assume conservation laws that do not hold in dissipative systems, leading to inconsistencies or limited applicability. Bateman¹ introduced a novel method that addresses this challenge by coupling the original system to a mirror counterpart that evolves in reverse time. This approach effectively conserves total energy, making canonical quantization viable. Over the years, this methodology has been adopted and extended in various works, particularly in quantum dissipation and thermo-field dynamics^2-7.

By doubling the degrees of freedom, the system’s dissipative behavior is embedded within a larger conservative framework, which allows the use of Hamiltonian mechanics for quantization. The Hamilton-Jacobi approach further provides a bridge between classical and quantum descriptions. Recent studies have applied this technique in diverse areas such as thermal field theory, decoherence, and the WKB approximation^8-11.

This study aims to explore the quantization of a damped harmonic oscillator using the degree-doubling technique. Through detailed derivations and transformations, it shows how this framework leads to a viable quantum model that excludes explicit damping terms and accurately reflects the physical behavior of the original system.

Hamilton’s principle: The study begins by applying Hamilton’s principle^10,11, which asserts that the actual trajectory followed by a mechanical system between two points in time is the one that minimizes the action, defined as the integral of the Lagrangian with respect to time. Mathematically, the action S is given by:

(1)

where, L represents the Lagrangian function of the system. To account for energy dissipation in the system, the model introduces a mirrored coordinate, denoted as y, which evolves in reverse time and is coupled with the original coordinate x. The modified Lagrangian accounts for both the original and mirrored dynamics and includes a damping term characterized by a damping coefficient, gamma (γ). The modified action integral becomes:

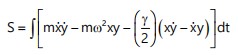(2)

where, m is the mass of the oscillator and ω is the natural angular frequency. By applying the principle of stationary action (δS = 0), we derive two coupled equations of motion:

(3)

(4)

These equations represent the damped oscillator (x) and its time-reversed counterpart (y). To simplify the analysis, we introduce two new generalized coordinates, defined as the symmetric and antisymmetric combinations of x and y:

(5)

(6)

By substituting these variables into the Lagrangian, and obtain:

(7)

From this, derives the corresponding Hamiltonian function, which governs the system’s total energy in terms of the conjugate momenta p_η and p_ξ:

(8)

Where:

	m	=	Mass of the oscillator
	ω	=	Angular frequency
	γ	=	Damping coefficient
	ξ and η	=	Transformed coordinates
	pξ and pη	=	Conjugate momenta associated with ξ and η, respectively

If uses the equations of transformation:

(9)

(10)

Then obtain the differential form of the Hamiltonian:

(11)

where, S is the Hamilton principal function.

The standard Hamilton-Jacobi equation for this Hamiltonian is given by:

(12)

By substituting Eq. 19 into Eq. 20:

(13)

Now can expand the variables in the usual way of separation used in the Hamilton-Jacobi equation by assuming that S is the sum of three terms:

S (ξ, η, t) = Wξ+Wη-α3t

(14)

Substituting Eq. 22 into Eq. 21, obtain the following differential equation for W_ξ and W_η:

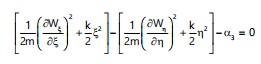(15)

This equation can be correct if both of the terms on the left-hand side are equal to a constant, since they are functions of different variables:

(16)

(17)

where, α₁, α₂ and α₃ are constants such that:

α3 = α1-α2

(18)

By integrating Eq. 24 and 25, obtain:

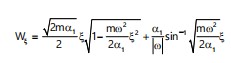(19)

And:

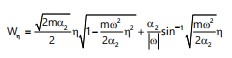(20)

Therefore:

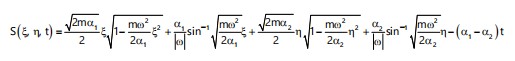(21)

The coordinate transformation successfully decouples the original dissipative dynamics into a conservative form. This allows for the application of canonical quantization, where classical momenta are replaced by quantum mechanical operators. In this framework, the Hamiltonian operator acts on the wave function Ψ, producing the Schrödinger equation:

(22)

Here, ħ is the reduced Planck constant, and Ĥ represents the Hamiltonian operator. The momentum operators in the Schrödinger picture are defined as:

(23)

(24)

as the Schrödinger’s equation associated with this system, where H is the Hermitian operator associated with the classical expression:

(25)

Hence:

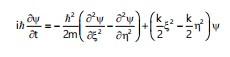(26)

Write:

(27)

Then we have:

(28)

If we assume that ħ→0, which is the classical limit in quantum mechanics, then we see that:

(29)

More generally:

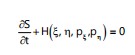(30)

which is just the Hamilton-Jacobi equation. Thus, in the classical limit ħ→0 the Schrödinger equation is just the Hamilton-Jacobi equation.

Returning to the Schrödinger equation:

(31)

and taking into account that:

(32)

Then have:

(33)

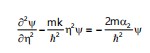(34)

Substituting back in Eq. 27:

(35)

Simplifying:

(36)

and finally:

(37)

Upon applying Schrödinger’s equation, it is found that the damping coefficient γ does not appear in the final expressions for energy eigenstates or time evolution. This result confirms that, at the quantum level, the dissipation is absorbed internally by the extended system via the auxiliary coordinate. Therefore, the approach of doubling the degrees of freedom provides a consistent method for quantizing non-conservative systems, such as damped harmonic oscillators.

CONCLUSION

This work demonstrates the effectiveness of the degree-doubling method in quantizing damped harmonic oscillators. The main contributions include the reformulation of a dissipative system into a conservative one and the validation of the method through canonical and Schrödinger quantization. While the model assumes linear damping and ideal coupling, future research may explore non-linear systems and environmental interactions. This framework could inform the quantization of broader classes of open systems.

SIGNIFICANCE STATEMENT

This study discovered the effectiveness of the degree-doubling method in reformulating damped harmonic oscillators as conservative systems suitable for quantization. This can be beneficial for advancing quantum models of open, dissipative systems using canonical and Schrödinger frameworks. The approach offers a consistent transition from classical to quantum descriptions by eliminating damping effects through a mirror system. This study will help researchers to uncover the critical areas of quantum dissipation and open-system dynamics that many were not able to explore. Thus, a new theory on open quantum systems may be arrived at.

REFERENCES

1. Bateman, H., 1931. On dissipative systems and related variational principles. Phys. Rev. 38: 815-819.
2. Caldeira, A.O. and A.J. Leggett, 1983. Path integral approach to quantum Brownian motion. Phys. A: Stat. Mech. Appl., 121: 587-616.
3. Caldeira, A.O. and A.J. Leggett, 1983. Quantum tunnelling in a dissipative system. Ann. Phys., 149: 374-456.
4. Celeghini, E., M. Rasetti and G. Vitiello, 1992. Quantum dissipation. Ann. Phys., 215: 156-170.
5. Calogeracos, A. and G. Barton, 1995. On the quantum electrodynamics of a dispersive mirror.: II. The boundary condition and the applied force via Dirac′s theory of constraints. Ann. Phys., 238: 268-285.
6. Nyffeler, A. and A. Schenk, 1995. Effective field theory of the linear O(N) sigma model. Ann. Phys., 241: 301-336.
7. Umezawa, H., H. Matsumoto and M. Tachiki, 1982. Thermo Field Dynamics and Condensed States. North-Holland, Netherlands, ISBN: 0444863613, Pages: 607.
8. Rabei, E.M., K.I. Nawafleh, and H.B. Ghassib, 2002. Quantization of constrained systems using the WKB approximation. Phys. Rev. A. 66: 024101-024101.
9. Nawafleh, K.I., E.M. Rabei and H.B. Ghassib, 2004. Hamilton-Jacobi treatment of constrained systems. Int. J. Mod. Phys. A, 19: 347-354.
10. Liu, G., Z.R. Lv and Y.M. Chen, 2018. Improving Wilson-θ and Newmark-β methods for quasi-periodic solutions of nonlinear dynamical systems. J. Appl. Math. Phys., 6: 1625-1635.
11. Goldstein, H., C.P. Poole and J.L. Safko, 2002. Classical Mechanics. 3rd Edn., Addison Wesley, Boston, USA, ISBN: 978-0201657029, Pages: 638.